Automates cellulaires 1D

Partie 1: Automates bicolores

Il s'agit de simuler l'évolution d'une colonie de cellules à une dimension,au cours du temps

Une cellule a deux états: soit elle est vivante ce qui est représenté par le nombre 1 et la couleur noire à l'écran

Soit elle n'existe pas ce qui représenté par le nombre 0 et la couleur blanche

A un instant t la colonie est représenté par un tableau de taille égale au nombre de cellules ici 300

A l'instant initial on va supposer qu'il y a une seule cellule vivante située au centre du tableau t

Pour passer d'un état au suivant voici comment on procède

1. On regarde pour chaque cellule t[i] le voisin de gauche t[i-1] et le voisin de droite t[i+1] et on forme un nombre binaire ainsi t[i-1]t[i]t[i+1]

   Ce nombre est compris entre 000 et 111 = 7. Pour chacun de ces nombres on définie une règle d'évolution par la donnée de soit 0 soit 1.

   Une règle d'évolution est donc une fonction allant de l'ensemble M des mots de longueur 3, de 000 à 111, vers l'ensemble {0,1}

   Il existe donc $2^{8} = 256$ règles d'évolution possibles

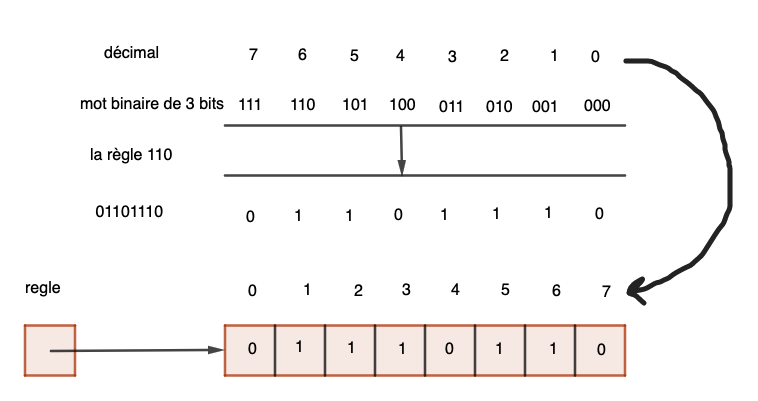
   Autrement dit une règle est définie par un octet, avec la convention suivante:

2. Par exemple la règle 110 est nommée ainsi car 110 en binaire correspond à l'octet 01101110 visualisé par

   

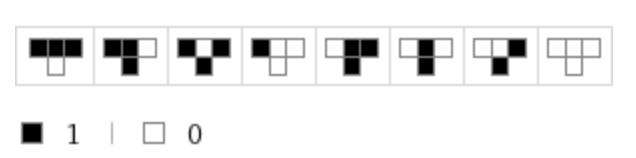
   Cet octet sera mémorisé par un tableau octet = [0,1,1,1,0,1,1,0], car la règle en tant que fonction, est l'association de l'indice i à la valeur octet[i]



3. Pour engendrer l'état suivant de la colonie, on utilise un nouveau tableau t'. On parcourt alors le tableau t associé à la colonie et chaque triplet (t[i-1],t[i],t[i+1]) correspond à un mot de 3 lettres en binaire correspondant à un indice j en décimal tel que l'état suivant de la cellule en i sera octet[j]

   Autrement dit t'[i] = octet[j]

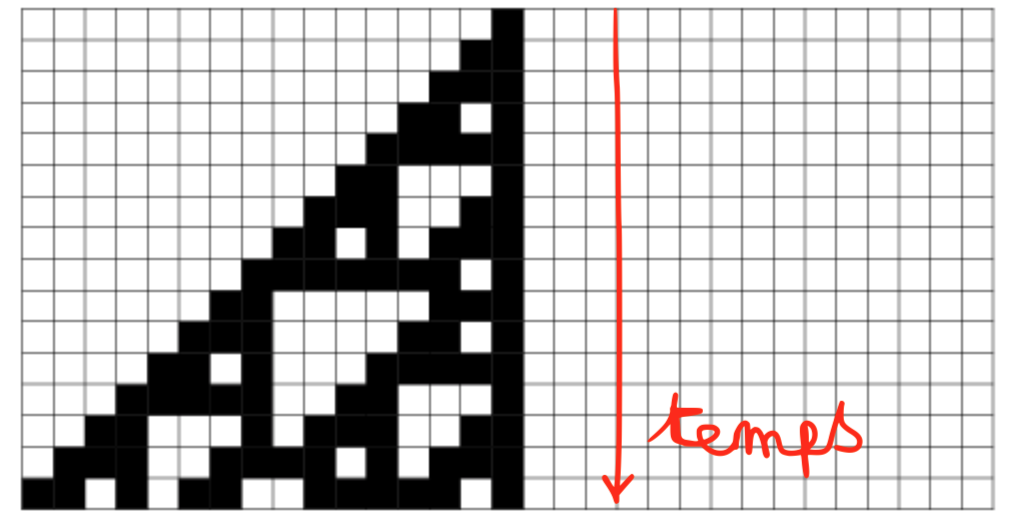
   Une fois t' rempli on le visualise juste en dessous de t

   

4. Ensuite t prend la valeur de t' et on répète le processus plusieurs fois

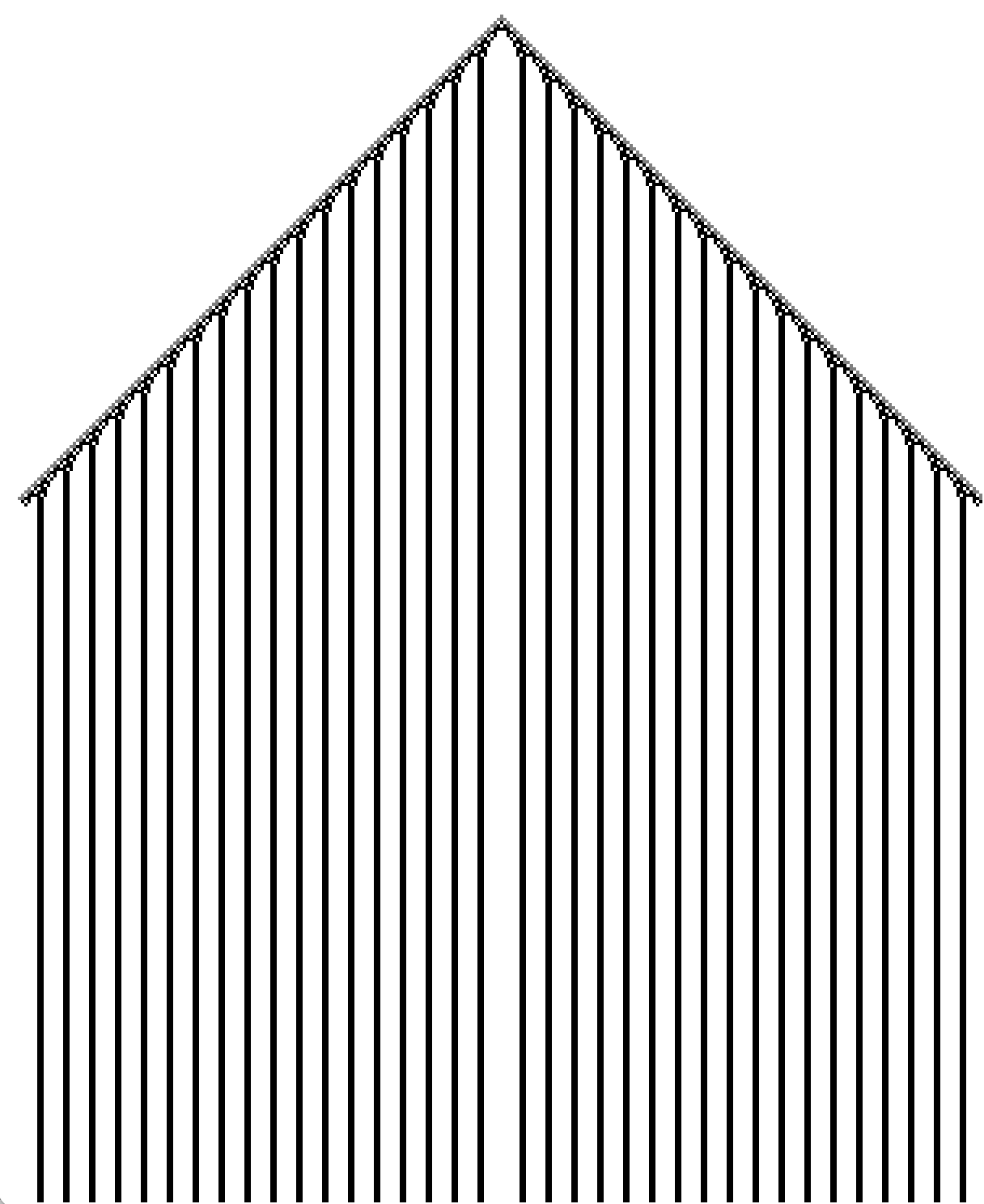
   Par exemple ci-dessous il y a 15 générations

   

5. Regardons de plus près la génération de la deuxième colonie sur Python Tutor

   		
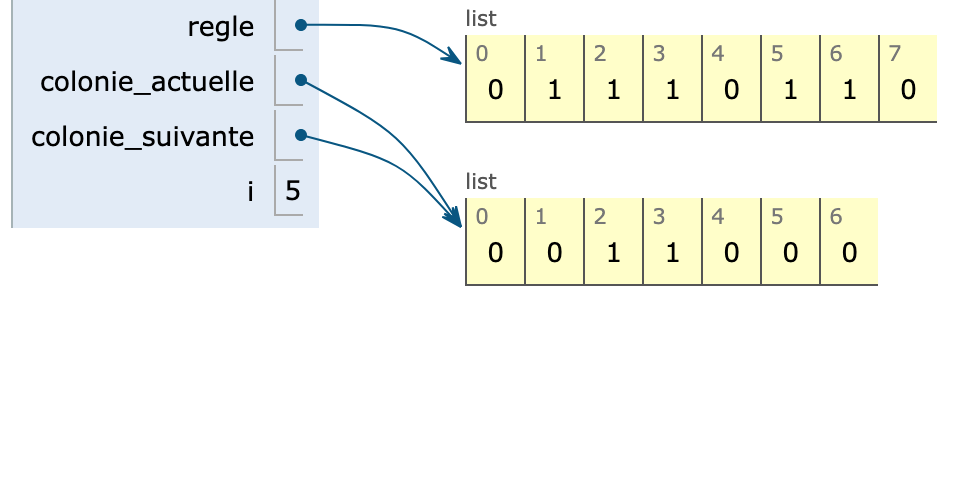
   def bin_to_dec(gauche,centre,droit):
   	return 2**2*gauche + 2*centre + droit
   
   regle = [0,1,1,1,0,1,1,0]
   colonie_actuelle = [0,0,0,1,0,0,0]
   colonie_suivante = [0]*7
   for i in range(1,len(colonie_actuelle)-1):
   	colonie_suivante[i] = regle[bin_to_dec(colonie_actuelle[i-1]),
   	colonie_actuelle[i],colonie_actuelle[i+1])]
   
   

   On observe :

   

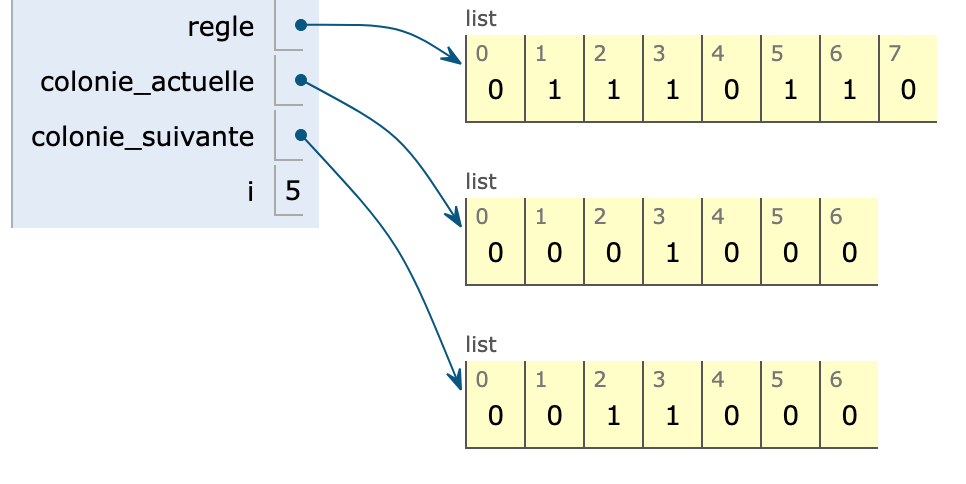
6. Pour genérer plusieurs colonies il suffit de rajouter à la fin de la boucle for l'instruction permettant de conserver dans colonie_actuelle la référence de colonie_suivante

   		
   def bin_to_dec(gauche,centre,droit):
   	return 2**2*gauche + 2*centre + droit
   
   regle = [0,1,1,1,0,1,1,0]
   colonie_actuelle = [0,0,0,1,0,0,0]
   colonie_suivante = [0]*7
   for i in range(1,len(colonie_actuelle)-1):
   	colonie_suivante[i] = regle[bin_to_dec(colonie_actuelle[i-1]),
   	colonie_actuelle[i],colonie_actuelle[i+1])]
   colonie_actuelle = colonie_suivante
   
   

   On observe :

   

Travail à faire

1. Le squelette du code est à télécharger ici
2. Compléter et tester les fonctions dec_to_bin et indice
3. Compléter et tester les fonctions communes aux automates bicolores et tricolores, initialisation, etat_suivant, generation_suivante et evolution

4. Dans le main tester la règle 110

   Lire les pages 54 à 59 de ce document et tester les automates visualisées dans ce document.

Partie 2: Automates tricolores

Maintenant une cellule peut avoir trois états numérotés 0,1 ou 2

Au nombre 2 est associée la couleur noire et au nombre 1, la couleur grise

Par contre l'état futur d'une cellule dépend de la somme des états des deux voisins et de la cellule elle même, donc au minimum c'est 0 au maximum c'est 6

Donc pour définir une règle d'évolution on va créer un tableau de longueur 7, d'indice 0 (pour la somme = 0) jusqu'à l'indice 6 ( pour la somme = 6)

A chaque cellule de ce tableau on peut associer l'une des trois valeurs 0, 1 ou 2

Autrement dit une règle d'évolution est un nombre sur 7 bits écrit en base 3

Il y a $3^7 = 2187$ règles possibles

Une règle sera donc caractérisée par un nombre entier entre 0 et 2186, qu'il faudra écrire en base 3 dans un tableau de taille 7

Travail à faire

1. Compléter et tester les fonctions dec_to_tri et indice_tri
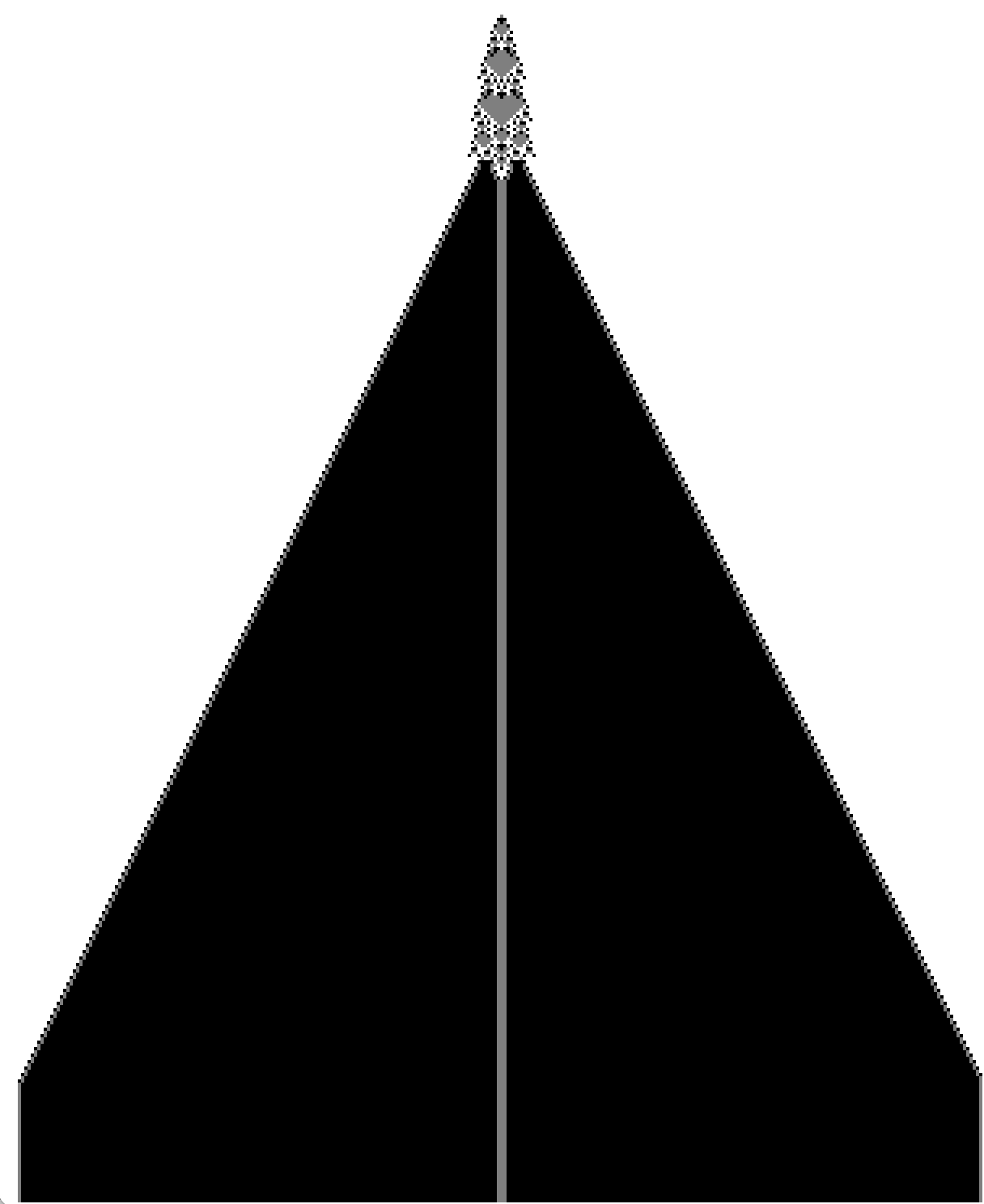
2. Visualiser les automates tricolores ci-dessous avec votre programme